“You don’t learn to walk by following rules. You learn by doing and falling over.”

Richard Branson

I’ve been studying in SIS KG for the past 10 years and 3/20 of this has been the experience of the IGCSE programme. The experience has been great. We are given tests, assignments and preparations to help us get ready for the IGCSE exams. For this term’s semester assignment we are given 3 investigations. Investigation A, B and C.

Part A: “Abigail”s airline”

In investigation A we were told to graph a line that would overlap the dotted lines on the runway. The topic involved was Linear Programming. We all know that an equation of a line is “y = mx+c” How I got the answer was first, I typed down “y = ”

• 

• 

Based on these pictures you could see the difference it would make if m is a positive number or a negative number. Then since i know that m is a negative number, I just trial and errored to find which negative number it’ll be. In this case it’s -4. To position the line in the correct place, I change “c” or so called the “y-intercept”. If c is anegative number, it’ll shift to the left and if c is a positive number the graph would shift to the right.

Part B: “Devloping Inquiry Skills”

In Investigation B, we are given the length of each side of the triangle is 81 cm. We were told to calculate the perimeter; area of the snowflake at each iteration. The topic involved is sequences.

Finding the perimeter at each oteration

The perimeter of the snowflake after n iterations is:

Pn = 3 * s * (4/3)^n

where s = side length of original triangle (81cm), n = no. of sides

---

So on the first iteration, the perimeter of the triangle is

3(81)*(4/3)^(0) = 243cm

Second iteration: 3(81)*(4/3)^(1)= 324cm

Third iteration: 3(81)*(4/3)^(2)= 432cm

Forth iteration: 3(81)*(4/3)^(3)= 576cm

Finding the area of the snowflake at each iteration

The are to find Koch’s snowflake at any given iteration is given by:

(2s^2√3)/5

where s = side length of original triangle (81cm)

So, the area is (2(81^2)(3^1/2))/5 = 4545.6 cm^2

Part C: “Sierpinski’s triangle”

1.

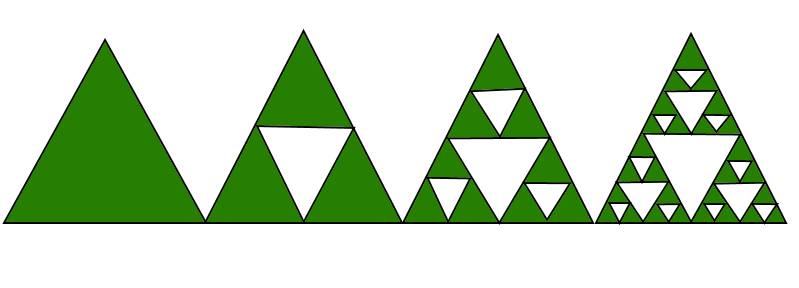
2.

3.

The pattern I obeserved in relation to the number of green triangles:

3^n

The pattern I observed in relation to the length of one side of one green triangle:

(1/2)^n

The pattern I observed in relation to the area of the green triangle:

(1/4)^n

Where n is the number of stages.

4.

I observed that all these patterns are arithmetic sequences, which uses “n” as the index.

5.

6.

As the number of stages increases, the length of one side of one green triangle decreases by a factor of 1/2, and the area of each green triangle decreases by a factor of 1/4.

Reflection

I have consequentluy learnt the IB learner profiles of being a thinker, because thinking helps define and organise esperiences, plan, leadrn, reflect and create; it is important that we make the best use of the gift of knowledge so that we achieve greay feats and heights in every way of our life; being open-minded helps us to learn and grow, strengthening your belief in yourself.

Unforgettable Moments

They say the small things in life are the most precious. They are the ones that make you smile and think how great life is. Your life is filled with moments you wish you could re-live over and over again. When i was in grade nine, I entered a mathematics competition with my classmates. After grinding at the competition for several hours, i finally managed to finsih the paper. I got pretty good scores for the past papers, so i figured I had it in the bag. Few months later when the results came, I got a bad score and didn’t make it to the next round. Welp I guess I still suck at guessing :3 but on the bright side, few of my friends made it to the next round and I’m proud of them. 😀

#IGCSEMath2020 #FirstBatch